タイトル:AIしてる?
探究領域:万象究理
セントラルアイディア:データには未来へのメッセージが宿る。
今週は確率の世界へと誘います。
まずは、データ読み取って予測を行う上で最も重要な法則である「大数(たいすう)の法則」を学びます。
まず、確率といえば、「コイン」、「サイコロ」。
コイン投げで出る目、つまり「表」の出る確率はどのくらいでしょうか?
二分の一、50%、5割、など様々な表現がありますが、キッズたちは聞くまでもなく、即答でした。
「確率」は「理屈」から考えられた「あるイベントの起こりやすさ」です。
たとえば、コイン投げで言えば、「裏と表の二つの選択肢のうちの一つが必ず出るから、二分の一、つまり50%である」という理屈に基づいて表の出る確率を考えることができます。
ではコインを投げてみると本当に50%は表になるのでしょうか?
そんな疑問から、実際にコインを一人100回投げてそれぞれ、表と裏が何回ずつどのような出方をするか、ひたすらコイン投げの実験をしました。

実験の結果は・・・
なんと、「48%」!!
1100回投げたうち、表が528回、裏が572回でて、表が出た割合は50%とはなりませんでした。
今回投げたコインは日本の10円玉だったのですが、経験則でいうならば「10円玉は表が出にくい」という結論になるはずです。
しかし、キッズたちはこの問いに対して、少々納得がいかない顔。
なぜか?を考えると「表の方が銅が少ない」「裏の方が重い」など、その細かい重さの違いが出目の「誤差」に出るということがあるのではないかという考えが出てきました。
では、回数が増えるに従って「表」が出る割合はどのように変動したのでしょうか?
どのようになったか、データを読み取るために、横軸に「回数」を、縦軸に「表の出た割合」を指定しグラフにしました。
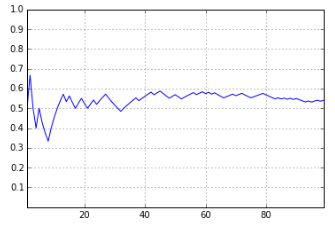
グラフを見て行くとはじめは60%になったり、20%になったり、理屈で考えていた「50%」の値とは遠い割合になっていましたが、回数を増すごとにだんだんと理屈で考えていた「50%」に近づきました。
こうした理屈からわかる「確率」と実験からわかる「割合」の間には「大数(たいすう)の法則」という関係性が成り立ちます。
「大数(たいすう)の法則」とは、データの数が増えれば増えるほど、その割合は確率に近づいていく法則です。
私たちは予測をするときに過去に取得されたデータからその発生割合を求めることができます。
しかし、得られたデータが少ないと、その「たまたま」度合いは高くなっていきます。
例えば、野球のバッターをイメージしてください。3打席で1安打を打った3割打者と、300打席で100安打を打った3割打者ではどちらが信頼できるでしょうか。
たくさんのデータを得ることで、その「たまたま」度合いを減らすことができ、例えば、野球のバッターならばその「本来の実力」、つまり、「本当の確率」に近いといえるのです。
では降水確率はどのように求められるのでしょうか。「ランダム」ではない事象について、来週からは、その「メカニズム」を探り、「理屈」から「確率」を考えます。
TY
※TCS2016年度探究テーマ一覧は、こちらよりご覧ください。
探究領域:万象究理
セントラルアイディア:データには未来へのメッセージが宿る。
[5・6年生]
今週は確率の世界へと誘います。
まずは、データ読み取って予測を行う上で最も重要な法則である「大数(たいすう)の法則」を学びます。
まず、確率といえば、「コイン」、「サイコロ」。
コイン投げで出る目、つまり「表」の出る確率はどのくらいでしょうか?
二分の一、50%、5割、など様々な表現がありますが、キッズたちは聞くまでもなく、即答でした。
「確率」は「理屈」から考えられた「あるイベントの起こりやすさ」です。
たとえば、コイン投げで言えば、「裏と表の二つの選択肢のうちの一つが必ず出るから、二分の一、つまり50%である」という理屈に基づいて表の出る確率を考えることができます。
ではコインを投げてみると本当に50%は表になるのでしょうか?
そんな疑問から、実際にコインを一人100回投げてそれぞれ、表と裏が何回ずつどのような出方をするか、ひたすらコイン投げの実験をしました。

実験の結果は・・・
なんと、「48%」!!
1100回投げたうち、表が528回、裏が572回でて、表が出た割合は50%とはなりませんでした。
今回投げたコインは日本の10円玉だったのですが、経験則でいうならば「10円玉は表が出にくい」という結論になるはずです。
しかし、キッズたちはこの問いに対して、少々納得がいかない顔。
なぜか?を考えると「表の方が銅が少ない」「裏の方が重い」など、その細かい重さの違いが出目の「誤差」に出るということがあるのではないかという考えが出てきました。
では、回数が増えるに従って「表」が出る割合はどのように変動したのでしょうか?
どのようになったか、データを読み取るために、横軸に「回数」を、縦軸に「表の出た割合」を指定しグラフにしました。

グラフを見て行くとはじめは60%になったり、20%になったり、理屈で考えていた「50%」の値とは遠い割合になっていましたが、回数を増すごとにだんだんと理屈で考えていた「50%」に近づきました。
こうした理屈からわかる「確率」と実験からわかる「割合」の間には「大数(たいすう)の法則」という関係性が成り立ちます。
「大数(たいすう)の法則」とは、データの数が増えれば増えるほど、その割合は確率に近づいていく法則です。
私たちは予測をするときに過去に取得されたデータからその発生割合を求めることができます。
しかし、得られたデータが少ないと、その「たまたま」度合いは高くなっていきます。
例えば、野球のバッターをイメージしてください。3打席で1安打を打った3割打者と、300打席で100安打を打った3割打者ではどちらが信頼できるでしょうか。
たくさんのデータを得ることで、その「たまたま」度合いを減らすことができ、例えば、野球のバッターならばその「本来の実力」、つまり、「本当の確率」に近いといえるのです。
では降水確率はどのように求められるのでしょうか。「ランダム」ではない事象について、来週からは、その「メカニズム」を探り、「理屈」から「確率」を考えます。
TY
※TCS2016年度探究テーマ一覧は、こちらよりご覧ください。
